39. Transformateur monophasé

Formule de Boucherot (valable au primaire et au secondaire)

Calcul de la f.e.m. induite (E) - Formule de Boucherot

\[ E = 4.44 \cdot \hat{B} \cdot N \cdot f \cdot S \]
  • E: f.e.m. induite par les variations de flux en volt (V)
  • \(\hat{B}\): Champ magnétique maximum en tesla (T)
  • N: nombre de spires
  • f: fréquence du courant en hertz (Hz)
  • S: section droite du circuit magnétique (m²)

Pour un TRANSFORMATEUR IDEAL

C'est-à-dire avec \(I_{1v} = 0A\) (courant primaire à vide considéré comme nul).

  • m: rapport de transformation

Rapport de transformation (m) - Transformateur idéal

\[ m = \frac{U_2}{U_1} = \frac{N_2}{N_1} = \frac{I_1}{I_2} \]

Rendement (η) - Transformateur idéal

\[ \eta = \frac{P_2}{P_1} = 100\% \]

Impédance de la charge vue du primaire (Z')

\[ Z' = \frac{Z}{m^2} \]
Grandeurs Primaires Grandeurs Secondaires Description
N1 N2 Nombre de spires
U1 U2 Tension (V)
I1 I2 Courant (A)
P1 P2 Puissance active (W)
Q1 Q2 Puissance réactive (Var)
S1 S2 Puissance apparente (VA)
\(\cos\phi_1\) \(\cos\phi_2\) Facteur de puissance
Z' Z Impédance de la charge (\(\Omega\))

Relations : * \(P_1 = P_2\) * \(Q_1 = Q_2\) * \(S_1 = S_2\) * \(\cos\phi_1 = \cos\phi_2\)

Schémas

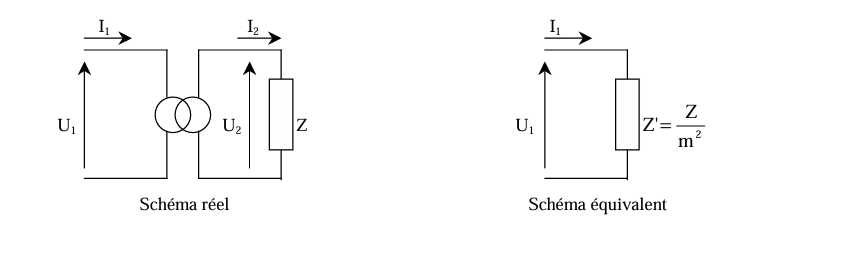
illustration_39_1

Schéma réel 

      I1                              I2
      +-------------------------------+--------------------------------+
      |                               |                                |
     ---                             ---                              ---
     | |                             | |                              | | Z (Charge)
 U1  | | N1                          | | N2                       U2  | |
     | |                             | |                              ---
     ---                             ---                               |
      |                               |                                |
      +-------------------------------+--------------------------------+

Schéma équivalent (vu du primaire) 

      I1
      +-------------------------------+
      |                               |
     ---                             ---
     | |                             | |
 U1  | | Z' = Z/m²                   | |
     | |                             | |
     ---                             ---
      |                               |
      +-------------------------------+

Pour un TRANSFORMATEUR REEL monophasé

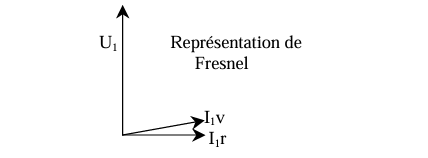
illustration_39_2

Avec \(I_{1v} \neq 0A\).

À vide (\(I_2 = 0A\))

Courant à vide (Approximation)

\[I_{1v} \approx I_{1r}\]

Rapport de transformation à vide (mv)

\[ m_v = \frac{U_{2v}}{U_1} = \frac{N_2}{N_1} \]
  • I1v = courant primaire à vide en ampère (A)
  • I1r = composante réactive du courant primaire à vide = courant magnétisant.
  • mv = rapport de transformation à vide
  • U2v = tension de sortie à vide en volt (V)

En charge (\(I_2 > 0A\))

Rapport de transformation en charge (m)

\[ m = \frac{I_1}{I_2} \]

Chute de tension absolue en sortie (ΔU2)

\[ \Delta U_2 = U_{2v} - U_2 \]

Chute de tension relative en sortie (ΔU2%)

\[ \Delta U_{2\%} = \frac{U_{2v} - U_2}{U_{2v}} \]

∆U2 = chute de tension absolue, en sortie et en charge (V)
U2v = tension au secondaire à vide en volt (V)
U2 = tension au secondaire en charge (V)
∆U2/U2v = chute de tension relative, en sortie et en charge, elle s’exprime en %. (en général < 4%)

Bilan des puissances

Rendement du transformateur (η)

\[ η = \frac{P_2}{P_1} \]

η = rendement du transformateur en %
P2 = puissance active fournie par le secondaire à la charge en watt (W) 1
P1 = puissance active absorbée par le primaire (W)
η ≈ 90% pour les petits transformateurs.
η > 99% pour les transformateurs de très grande puissance.

Puissance active fournie par le secondaire (P2)

\[ P_2 = U_2 \cdot I_2 \cdot \cos\phi_2 \]

U2 = tension au secondaire en charge (V)
I2 = courant absorbé par la charge au secondaire (A)
cosϕ2 = facteur de puissance de la charge

Puissance active absorbée par le primaire (P1)

\[ P_1 = P_2 + P_F + P_j \]
\[ P_h = K_1 \cdot V \cdot f \cdot \hat{B}^2 \]
\[ P_f = K_2 \cdot V \cdot f^2 \cdot \hat{B}^2 \]
\[ P_j = R_1 I_1^2 + R_2 I_2^2 \]

\(P_F\): Pertes fer totales (pertes constantes, déterminées par essai à vide) (W).
\(P_j\): Pertes joule (pertes cuivre, déterminées par essai en court-circuit) (W).
\(P_h\): Pertes par hystérésis (W).
\(P_f\): Pertes par courants de Foucault (W).
\(K_1, K_2\): Constantes liées au circuit magnétique.
V: Volume du circuit magnétique (m³).
f: Fréquence du courant (Hz).
\(\hat{B}\): Champ magnétique maximum (T).