29. Circuit R.L.C.

RLC en Série vs. Parallèle

Réactor de Résistance R($\Omega$), Bobine d’inductance L(H), Condensateur de capacité C(F) en courant alternatif sinusoïdal monophasé.

RLC en Série	RLC en Parallèle


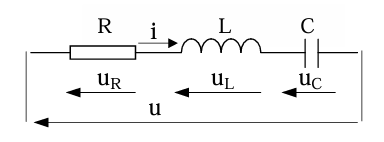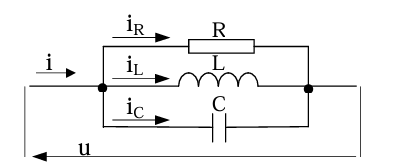i est commun	u est commun
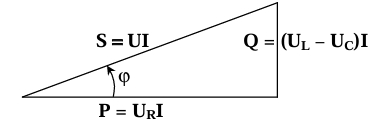
Triangle des tensions	Triangle des courants
$\vec{U} = \vec{U_R} + \vec{U_L} + \vec{U_C}$	$\vec{I} = \vec{I_R} + \vec{I_L} + \vec{I_C}$

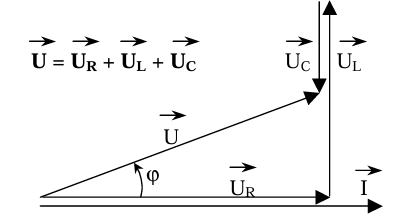Triangle des impédances (Série) vs. Admittances (Parallèle)

RLC en Série	RLC en Parallèle
Triangle des impédances Z($\Omega$)	Triangle des admittances Y(S) (S = siemens = $\Omega^{-1}$)

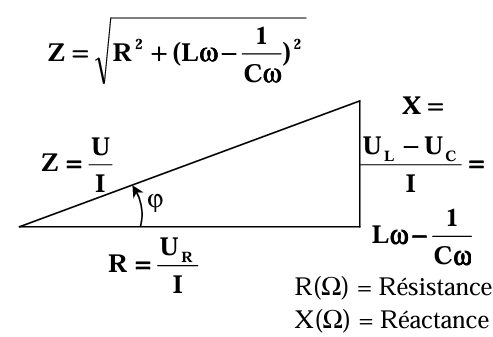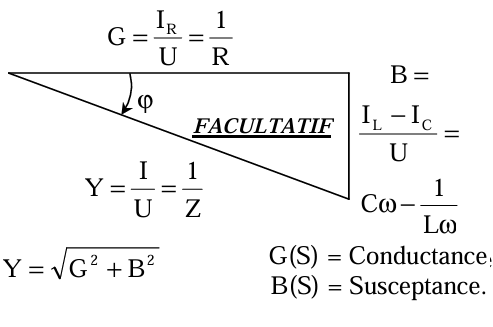$$ Z = \sqrt{R^2 + (L\omega - \frac{1}{C\omega})^2} $$	$$ Y = \sqrt{G^2 + B^2} $$
$$ Z = \frac{U}{I} $$	$$ Y = \frac{I}{U} = \frac{1}{Z} $$
$$ R = \frac{U_R}{I} $$ (Résistance)	$$ G = \frac{I_R}{U} = \frac{1}{R} $$ (Conductance)
$$ X = X_L - X_C = L\omega - \frac{1}{C\omega} $$ (Réactance)	$$ B = B_C - B_L = C\omega - \frac{1}{L\omega} $$ (Susceptance)

Circuit Résonnant (Série) vs. Circuit Bouchon (Parallèle)

Il y a résonance (série) ou circuit bouchon (parallèle) si :

Condition de résonance (série) ou circuit bouchon (parallèle)

\[X_L = X_C \Rightarrow L\omega = \frac{1}{C\omega } \Rightarrow LC\omega^2 = 1 \Rightarrow \cos\phi = 1\]

Triangle des puissances

RLC en Série	RLC en Parallèle
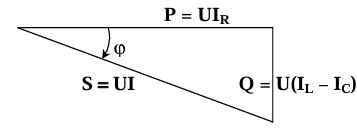
$$ S = U \cdot I $$	$$ S = U \cdot I $$
$$ P = U_R \cdot I $$	$$ P = U \cdot I_R $$
$$ Q = (U_L - U_C)I $$	$$ Q = U(I_L - I_C) $$

Remarque : On obtient la même chose avec le montage série et parallèle :

Calcul de la puissance apparente (S) dans le triangle des puissances

\[ S = \sqrt{P^2 + Q^2}\]

Formules générales (Montage Monophasé)

Formule de la Puissance apparente (S)

\[ S = U \cdot I \]

S : Puissance apparente Volt Ampère (VA)

Formule de la Puissance active (P)

\[ P = U \cdot I \cdot \cos\phi \]

P : Puissance active en Watt (W)

Formule de la Puissance réactive (Q)

\[ Q = U \cdot I \cdot \sin\phi \]

Q : Puissance réactive en Volt Ampère Réactif (VAR)

Formule du Facteur de puissance (cos ϕ)

\[ \cos\phi = \frac{P}{S} = \frac{R}{Z} \]

cos ϕ : Facteur de puissance

Loi d’ohm

\[ U = Z \cdot I \]

⇒⇒⇒ Loi d’ohm

Méthode de Boucherot

Quelque soit le couplage (série, parallèle ou mixte), les puissances actives (P) et réactives (Q) s’additionnent séparément. Les puissances apparentes (S) ne peuvent pas s’additionner directement. Elles se calculent par :

Théorème de Boucherot pour le calcul de la puissance apparente totale

\[ S = \sqrt{P^2 + Q^2} \]

(sans puissance déformante).

En présence de Puissance Déformante

Calcul des puissances en présence de puissance déformante (D)

\[ D = \sqrt{S^2 - P^2 - Q^2}\]

\[ S = \sqrt{P^2 + Q^2 + D^2}\]

D: puissance déformante en Volt Ampère Déformant (VAD). (Générée par les harmoniques, elle se représente verticalement au plan du triangle.)